반응형
시간 복잡도는 알고리즘의 효율성을 평가하는 중요한 척도이다. 주어진 입력 크기 n에 따라 알고리즘이 실행되는 데 걸리는 시간을 수학적으로 표현한 것이다. 이를 통해 알고리즘이 커지는 입력에 대해 얼마나 효율적인지 판단할 수 있다.
시간 복잡도 종류
- O(1): 상수 시간 복잡도
- 입력 크기에 상관없이 실행 시간이 일정하다.
- 예: 배열에서 첫 번째 요소를 읽는 작업
- 이 코드는 입력 크기에 상관없이 언제나 한 번만 실행되므로 시간 복잡도는 O(1)이다. n이 커져도 동일한 작업을 하며, 실행 시간이 변하지 않는다.
public class ConstantTime {
public static void main(String[] args) {
int n = 100;
System.out.println("첫 번째 요소: " + n);
}
}- O(n): 선형 시간 복잡도
- 입력 크기 n에 비례하여 실행 시간이 증가한다.
- 예: 배열을 한 번 순회하는 작업
- 이 코드에서 for 루프는 배열의 길이만큼 반복된다. 즉, 배열의 크기가 커지면 반복 횟수도 비례하여 증가하므로 시간 복잡도는 O(n)이다.
public class LinearTime {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5};
for (int i = 0; i < arr.length; i++) {
System.out.println("요소: " + arr[i]);
}
}
}- O(log n): 로그 시간 복잡도
- 입력 크기가 증가할수록 실행 시간이 느리게 증가한다. 매번 입력 크기를 절반으로 줄이는 방식의 알고리즘에서 자주 나타난다.
- 예: 이진 탐색
- 이 코드는 binarySearch를 사용하여 배열에서 특정 요소를 찾는다. 이진 탐색은 매번 배열을 절반으로 나누기 때문에 시간 복잡도는 O(log n)이다. 배열의 크기가 커져도 비교 횟수는 로그에 비례하여 증가한다.
import java.util.Arrays;
public class LogarithmicTime {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
int key = 5;
int result = Arrays.binarySearch(arr, key);
System.out.println("키의 위치: " + result);
}
}- O(n²): 이차 시간 복잡도
- 입력 크기 n에 비례하여 제곱으로 실행 시간이 증가한다. 중첩된 반복문에서 주로 발생한다.
- 예: 버블 정렬, 선택 정렬
- 여기서는 이중 for 루프가 사용되었으므로 배열의 크기가 증가하면 반복 횟수는 입력 크기 n의 제곱에 비례한다. 시간 복잡도는 O(n²)이다.
public class QuadraticTime {
public static void main(String[] args) {
int[][] matrix = {{1, 2}, {3, 4}};
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[i].length; j++) {
System.out.println("요소: " + matrix[i][j]);
}
}
}
}- O(2^n): 지수 시간 복잡도
- 입력 크기가 조금만 커져도 실행 시간이 매우 빠르게 증가한다. 재귀적 문제 풀이에서 자주 나타난다.
- 예: 재귀적인 피보나치 수열 계산
- 이 코드에서 피보나치 수열을 재귀적으로 계산하는 알고리즘은 매우 비효율적이다. 동일한 값을 여러 번 계산하기 때문에 시간 복잡도는 O(2^n)이다.
import java.util.Arrays;
public class NLogNTime {
public static void main(String[] args) {
int[] arr = {5, 3, 1, 6, 4, 2};
Arrays.sort(arr);
System.out.println("정렬된 배열: " + Arrays.toString(arr));
}
}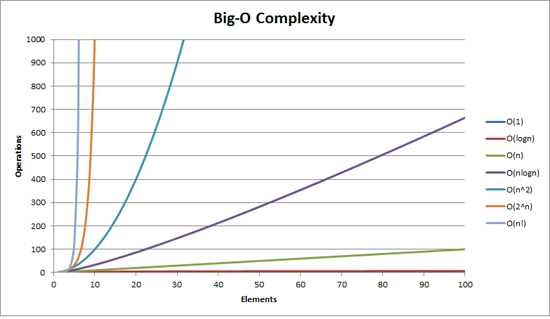
빅오 표기법(Big-O Notation)
시간 복잡도는 빅오 표기법으로 표현한다. 빅오 표기법은 알고리즘의 최악의 경우에 대한 실행 시간을 나타내며, 입력 크기 n이 매우 커질 때 성능을 평가하는 데 사용된다. 이 표기법은 입력 크기 증가에 따른 주요 성능 패턴을 설명하는 데 유용하며, 미세한 상수 시간이나 작은 차이는 무시한다.
예를 들어, O(2n + 3)이라는 표현이 있을 때, 이는 결국 큰 입력에서 선형적으로 동작하므로 *O(n)* 으로 간략화된다.
중요성
시간 복잡도는 알고리즘의 효율성을 평가하는 핵심 지표이다. 같은 문제를 해결하는 다양한 알고리즘 중에서 시간 복잡도가 작은 알고리즘을 선택하면 큰 입력에 대해 더 빠른 성능을 보일 수 있다.
반응형
'Algorithm > 개념정리' 카테고리의 다른 글
| [알고리즘] 삽입 정렬 정리 (2) | 2024.09.19 |
|---|---|
| [알고리즘] 순열(permutation)과 조합(Combination) 정리 (5) | 2022.10.03 |
| [알고리즘] 탐욕 (Greedy) 알고리즘 (2) | 2022.09.27 |
| [알고리즘] 시간복잡도 (Time Complexity) 개념 정리 (0) | 2022.09.27 |